2.1.1 Väändenurga elastse joone diferentsiaalvõrrand

Õhukeseseinalise varda takistatud väände diferentsiaalvõrrandi tuletamist alustame määrangust (1.27)

$${T_{sum}} = {T_{x\hspace*{1pt}t}} + {T_{x\hspace*{1pt}\omega}} %\cdot$$ (2.1)

kus

T_sum – koguväändemoment;

T_t – vabaväändemoment (väändemoment St. Venant'i väändel);

T_ω – kooldeväändemoment (kooldenihkepingetele vastav väändemoment).

Vabaväändemoment T_t  ja väändenurk θ on seotud avaldisega (1.1)

$${T_{x\hspace*{1pt}t}} = GI_{t}\theta^{\prime}$$ (2.2)

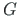kus $G$ on nihkeelastsusmoodul e nihkemoodul e Coulomb'i moodul ja I_t on väändeinertsimoment.

Bimomendi B_ω  ja väändenurga tuletis 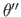$\theta^{\prime\prime}$ on seotud avaldisega (1.19)

$$B_{\omega} = -\hspace*{1pt}EI_{\omega}\hspace*{1pt}\theta^{\prime\prime}$$ (2.3)

Kooldeväändemoment T_ω  ja väändenurk 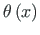$\theta\left(x\right)$ on seotud avaldisega (1.43)

$${T_{\omega}} = -\hspace*{1pt}E\hspace*{1pt}I_{\omega}\theta^{\prime\prime\prime}$$ (2.4)

kus E on (normaal)elastsusmoodul (Youngi moodul) ja I_ω on sektorinertsimoment (A.60).

Koguväändemomendi T_sum ja lausmomendi 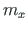$m_{x}$ vaheline seos (1.45):

$$\frac{{\mathrm{d}T_{sum}}}{{\mathrm{d}x}} = - {m_{x}}$$ (2.5)

Diferentseerime võrrandit (2.1) x-koordinaadi järgi:

$$- \hspace*{1pt}\frac{{T_{x\hspace*{1pt}t}}}{\mathrm{d}x} - \hspac... ...t}\omega}}}{\mathrm{d}x} = - \hspace*{1pt}\frac{{T_{sum}}}{\mathrm{d}x} %\cdot$$ (2.6)

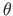Asendame võrrandis (2.6) väändemomendid väändenurga $\theta$ avaldistega ja lausmomendiga $m_{x}$:

$$E\hspace*{1pt}I_{\omega}\frac{\mathrm{d^{4}}\theta}{\mathrm{d}x^{... ...ce*{1pt}GI_{t}\frac{\mathrm{d^{2}}\theta}{\mathrm{d}x^{2}} = \hspace*{1pt}m_{x}$$ (2.7)

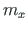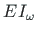Saadud võrrandi jagame kooldejäikusega $E\hspace*{1pt}I_{\omega}$ (sks Wölbsteifigkeit, ingl warping rigidity, vn ):

$$\frac{\mathrm{d^{4}}\theta}{\mathrm{d}x^{4}} - \hspace*{1pt}\frac... ...}\theta}{\mathrm{d}x^{2}} = \hspace*{1pt}\frac{m_{x}}{E\hspace*{1pt}I_{\omega}}$$ (2.8)

Võtame kasutusele õhukeseseinalise varda takistatud väänet iseloomustava karakteristiku κ, mida edaspidi nimetame kooldekarakteristikuks (sks Abklingfaktor für Torsion, ingl flexural-torsion cross-section characteristic, vn ):

$${\kappa} = {}\hspace*{1pt}\sqrt{\frac{GI_{t}}{E\hspace*{1pt}I_{\o... ...qquad \quad {a} = {}\hspace*{1pt}\sqrt{\frac{E\hspace*{1pt}I_{\omega}}{GI_{t}}}$$ (2.9)

kus

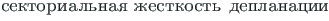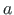${a}$ – kooldekarakteristiku pöördväärus (ingl torsional bending constant) [HIM11];

EI_ω – kooldejäikus;

GI_t – vabaväändejäikus (sks Torsionssteifigkeit, ingl torsional rigidity, vn ).

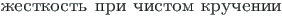Õhukeseseinalise varda takistatud väänet iseloomustava karakteristikuna on kasutusel ka varda tunnusarv väändel ε_t (sks Stabkennzahl für Torsion, ingl torsion parameter e warping parameter, vn ).

$${\epsilon_{t}} = {}l\hspace*{1pt}\sqrt{\frac{GI_{t}}{E\hspace*{1pt}I_{\omega}}}$$ (2.10)

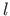kus ${l}$ on varda pikkus.

Nüüd esitame diferentsiaalvõrrandi (2.8) kujul

$${\theta}^{IV} - \hspace*{1pt}{{\kappa}}^{2}{\theta}^{\prime\prime} = \hspace*{1pt}\frac{m_{x}}{E\hspace*{1pt}I_{\omega}}$$ (2.11)