Järgmine: 2.1.5 Diferentsiaalvõrrandi erilahendid Üles: 2.1 Takistatud väände diferentsiaalvõrrandid Eelmine: 2.1.3 Väändenurga elastse joone
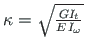 .
.
Lahendite süsteemi (2.24) normeerimiseks kirjutame välja
Wronski2.2 determinandi2.3:
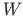 väärtus kohal
väärtus kohal 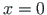 :
:
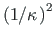 ;
;
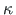 -ga korrutatud teise veeru, seejärel
korrutame neljanda veeru suurusega
-ga korrutatud teise veeru, seejärel
korrutame neljanda veeru suurusega
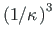 .
.
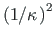 ;
; 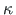 -ga korrutatud teise veeru, seejärel
korrutame neljanda veeru suurusega
-ga korrutatud teise veeru, seejärel
korrutame neljanda veeru suurusega
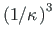 .
.
Varda sisejõudude leidmisel kasutatakse rajajõudude (kontaktjõudude)
märgikokkulepet (jn 1.17).
Esimese märgikokkuleppe puhul
Asendame avaldises (2.32) kooldejäikuse pöördväärtuse (1/
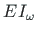 )
seosega (2.9) (
)
seosega (2.9) (
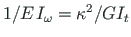 ).
).
andres