Järgmine: 2. Takistatud väände võrrandid Üles: 1. Põhimõisted Eelmine: 1.10.3 Pikikoormuse ülekandmine elastsele
| Toe skeem | Rajatingimus | Toe kirjeldus |
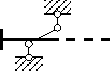
|
θ = 0 |
Jäik tugi ei võimalada
|
| θ' = 0 | ||
![\includegraphics[width=26mm]{joonised/Toed1.eps}](imgPtk1v274.png)
|
θ = 0 |
Tugi ei võimalda pööret; |
| Bω = 0 | ||
![\includegraphics[width=26mm]{joonised/Toed2.eps}](imgPtk1v275.png)
|
θ' = 0 |
Tugi võimaldab pööret; |
| Tω = 0 | ||
![\includegraphics[width=26mm]{joonised/Toed3.eps}](imgPtk1v276.png)
|
Bω = 0 |
Vaba ots |
| Tsum = Tt + Tω = M | ||
![\includegraphics[width=26mm]{joonised/Toed4.eps}](imgPtk1v277.png)
|
θ' = 0 |
Tugi võimaldab pööret; |
| Tω = M | ||
![\includegraphics[width=26mm]{joonised/Toed5.eps}](imgPtk1v278.png)
|
Bω = 0 |
Vabale otsale on rakendatud |
| Tsum = Tt + Tω = M |
Rajatingimuste seadmisel tuleb arvestada energiateoreemis (B.8) leitud rajatingimusi:
 ,
,
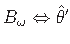 ,
,
 üks suurus on ette antud, siis teine on tundmatu, mis tuleb leida. Nii näiteks on tabelis 1.2 jäiga toe puhul
antud
üks suurus on ette antud, siis teine on tundmatu, mis tuleb leida. Nii näiteks on tabelis 1.2 jäiga toe puhul
antud 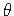 ja
ja 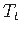 . Tundmatuks on
. Tundmatuks on
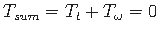 ,
kus
,
kus 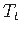 on antud, ning järelikult
on antud, ning järelikult
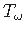 tuleb leida.
tuleb leida.
andres