Järgmine: 3.1.2 Murtud teljega L-tala Üles: 3.1 Rajatingimused Eelmine: 3.1 Rajatingimused
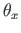 , vabaväändemomendi
, vabaväändemomendi 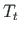 , bimomendi
, bimomendi
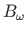 ja
kooldeväändemomendi
ja
kooldeväändemomendi
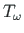 epüürid.
epüürid.
Andmed. Jätkuvtala avad
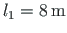 ,
,
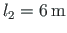 ja konsooli pikkus
ja konsooli pikkus
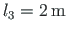 . Tala
esimene ava on koormatud ühtlase lausmomendiga
. Tala
esimene ava on koormatud ühtlase lausmomendiga
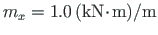 .
Tala teise ava keskele on rakendatud moment
.
Tala teise ava keskele on rakendatud moment
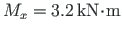 . Konsooli otsas
mõjub bimoment
. Konsooli otsas
mõjub bimoment
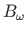
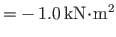 .
Ristlõikeks on valitud I-profiil nr 60a [Bõt62, lk 435].
Ristlõike kooldetugevusmoment
.
Ristlõikeks on valitud I-profiil nr 60a [Bõt62, lk 435].
Ristlõike kooldetugevusmoment
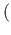
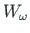
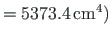 , paindejäikus
, paindejäikus
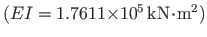 ,
kooldejäikus
,
kooldejäikus
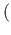
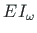
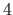 ,
vabaväändejäikus
,
vabaväändejäikus
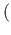
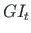
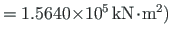 ja
kooldekarakteristik
ja
kooldekarakteristik
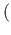
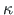
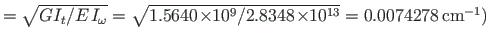 on konstantsed.
on konstantsed.
Lahendus. Toetingimuste seadmisel on arvestatud energiateoreemi (B.8)
Siit saab jälgida, milline toetingimus on antud ja milline leitakse.
Esimese toe toetingimuste paarides
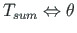 ja
ja
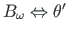 on antud väändenurk
on antud väändenurk 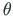
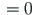 ja suhteline väändenurk
ja suhteline väändenurk
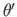
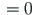 . Seega on esimene tugi jäik ning ei võimalda pööret ega kooldumist.
Tundmatud on bimoment
. Seega on esimene tugi jäik ning ei võimalda pööret ega kooldumist.
Tundmatud on bimoment
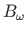 ja koguväändemoment
ja koguväändemoment 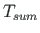 .
Varda lõpus on antud bimoment
.
Varda lõpus on antud bimoment
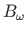
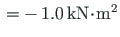 ja koguväändemoment
ja koguväändemoment 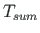
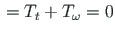 . Tundmatuks jäävad väändenurk
. Tundmatuks jäävad väändenurk 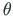 ja suhteline väändenurk
ja suhteline väändenurk
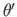 (
(
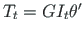 ).
).
Teisel ja kolmandal toel on varrassüsteemi elemente ühendavad sisesidemed ja välissidemed.
Välissidemeks on antud väändenurk 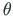
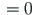 . Tundmatu on toemoment,
mis on võrdne elementide koguväändemomentide
. Tundmatu on toemoment,
mis on võrdne elementide koguväändemomentide 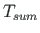 summaga.
Elemente ühendavateks sisesidemeteks on väändenurkade
summaga.
Elemente ühendavateks sisesidemeteks on väändenurkade 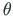 võrdsus ja suhteliste
väändenurkade
võrdsus ja suhteliste
väändenurkade
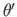 võrdsus. Samal ajal peavad elementide bimomendid
võrdsus. Samal ajal peavad elementide bimomendid
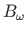 , koguväändemomendid
, koguväändemomendid 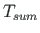 ja toemoment olema sõlmes tasakaalus.
ja toemoment olema sõlmes tasakaalus.
Rajaväärtuste arvutamiseks kasutame nagu EST-meetodi [Lah97a], [Lah14]
puhulgi hõredat võrrandisüsteemi 3.9
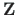 on võrrandisüsteemi tundmatute vektor
on võrrandisüsteemi tundmatute vektor
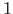 ,
, 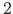 ja
ja 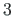 alguses ja lõpus
(jn 3.5):
alguses ja lõpus
(jn 3.5):
Muutuja
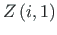 indeks (i=1, 2, 3,
indeks (i=1, 2, 3,  , 24) on näidatud joonisel 3.5.
, 24) on näidatud joonisel 3.5.
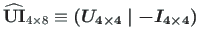 (2.87)
arvutamiseks saab kasutada GNU Octave'i funktsiooni yspWGvfmhvI.m .
(2.87)
arvutamiseks saab kasutada GNU Octave'i funktsiooni yspWGvfmhvI.m .
Võrrandisüsteemis (3.11) on tundmatuid poole rohkem kui võrrandeid. Kanname need võrrandid võrrandisüsteemi (3.6) (vt väljavõte programmist 3.1).
# Esimese tala hõreda laiendatud ülekandemaatriksi arvutus
spvF=yspWGvfmhvI(baasi0,l1,GIt,EIw);
vB1=yzWGmx(baasi0,l1,l1,a1,mx,GIt,EIw); # koormusvektori arvutus
IIv=1;
IJv=1;
vB1=vB1.*(-1);
# sisestab ülekandemaatriksi võrrandisüsteemi spA*Z=Bvb
spA=spInsertBtoA(spA,IIv,IJv,spvF);
# sisestab koormusvektori võrrandisüsteemi vabaliikmesse Bvb
Bvb=InsertBtoA(Bvb,NNK,1,IIv,1,vB1,4,1);
# Teise tala hõreda laiendatud ülekandemaatriksi arvutus
spvF=yspWGvfmhvI(baasi0,l2,GIt,EIw);
vB2=yzWGMx(baasi0,l2,l2,a2,Mx2,GIt,EIw); # koormusvektori arvutus
krda=2;
IIv=krda*8-7;
IJv=krda*16-15;
# sisestab ülekandemaatriksi võrrandisüsteemi spA*Z=Bvb
spA=spInsertBtoA(spA,IIv,IJv,spvF);
# sisestab koormusvektori võrrandisüsteemi vabaliikmesse Bvb
Bvb=InsertBtoA(Bvb,NNK,1,IIv,1,vB2,4,1);
# Kolmanda tala hõreda laiendatud ülekandemaatriksi arvutus
spvF=yspWGvfmhvI(baasi0,l3,GIt,EIw);
krda=3;
IIv=krda*4-3;
IJv=krda*8-7;
# sisestab ülekandemaatriksi võrrandisüsteemi spA*Z=Bvb
spA=spInsertBtoA(spA,IIv,IJv,spvF);
# võrrandisüsteemi vabaliige Bvb on eelnevalt nullitud
Võrrandisüsteemis (3.6) peab olema võrrandeid ja tundmatuid ühepalju. Võrrandite arv
peab ühtima maatriksi
 astakuga. Puuduvad sõltumatud võrrandid saame
kinemaatilistest ja staatilistest rajatingimustest (vt jaotis 3.1).
astakuga. Puuduvad sõltumatud võrrandid saame
kinemaatilistest ja staatilistest rajatingimustest (vt jaotis 3.1).
Järgnevalt
Rajatingimuste püstitus. Väliste rajatingimuste seadmisel sõlmedes
tuleb arvestada energiateoreemi 3.11 (![]() ).
Kui avaldistes
).
Kui avaldistes
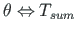 ,
,
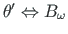 üks pool (pöördenurk
üks pool (pöördenurk 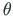 , suhteline väändenurk
, suhteline väändenurk
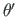 ) on antud, siis teine pool (koguväändemoment
) on antud, siis teine pool (koguväändemoment 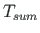 , bimoment
, bimoment
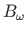 ) on tundmatu.
) on tundmatu.
Talal on sõlmes 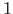 jäik tugi, mis ei võimalda pööret ega kooldumist (vt tabel 1.2).
Tundmatud on bimoment
jäik tugi, mis ei võimalda pööret ega kooldumist (vt tabel 1.2).
Tundmatud on bimoment
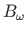 , toemoment
, toemoment 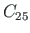 (vt jn 3.5)
ja koguväändemoment
(vt jn 3.5)
ja koguväändemoment
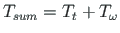 .
Viimases on vabaväändemoment
.
Viimases on vabaväändemoment
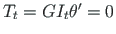 antud. Tundmatuks jääb kooldeväändemoment
antud. Tundmatuks jääb kooldeväändemoment
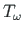 .
Teisel ja kolmandal toel on antud pöördenurk
.
Teisel ja kolmandal toel on antud pöördenurk 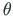 . Tundmatuks jäävad toemomendid
. Tundmatuks jäävad toemomendid 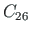 ja
ja 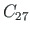 .
Tala otsas, sõlmes
.
Tala otsas, sõlmes 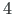 , on antud bimoment
, on antud bimoment
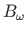 ja koguväändemoment
ja koguväändemoment
 .
Tundmatud on pöördenurk
.
Tundmatud on pöördenurk 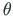 ja suhteline väändenurk
ja suhteline väändenurk
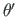 (
(
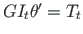 ).
).
Sisemistest rajatingimustest vaatleme sõlmede 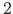 ja
ja 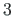 pidevustingimusi.
Varraste
pidevustingimusi.
Varraste 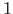 ja
ja 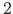 ning
ning 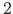 ja
ja 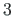 väändenurgad ja kooldumus 3.12 on võrdsed.
väändenurgad ja kooldumus 3.12 on võrdsed.
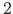 ja
ja 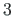 tasakaalutingimusi.
Tasakaalus peavad olema bimomendid, koguväändemomendid ja toeväändemomendid.
tasakaalutingimusi.
Tasakaalus peavad olema bimomendid, koguväändemomendid ja toeväändemomendid.
Koostatud on 16 rajatingimuse võrrandit. Sisestame need võrrandisüsteemi (3.6) (vt väljavõte programmist 3.2). Võrrandisüsteemi astak võrdub tundmatute arvuga. Järelikult on sisestatud võrrandid lineaarselt sõltumatud.
########## Rajatingimused
# Pidevustingimused
# Sõlm 2
spA=spSisestaArv(spA,13,5,1); # $theta_{5}$ on võrdne
spA=spSisestaArv(spA,13,9,-1); # $theta_{9}$ väändenurgaga
spA=spSisestaArv(spA,14,6,1); # $T_{t6}$ on võrdne
spA=spSisestaArv(spA,14,10,1); # $T_{t10}$
# Sõlm 3
spA=spSisestaArv(spA,15,13,1); # $theta_{13}$ - väändenurk
spA=spSisestaArv(spA,15,17,-1); # võrdne $theta_{17}$ väändenurga
spA=spSisestaArv(spA,16,14,1); # $T_{t14}$ on võrdne
spA=spSisestaArv(spA,16,18,1); # $T_{t18}$
# Tasakaalutingimused
# Sõlm 1
spA=spSisestaArv(spA,17,2,1); # $T_{t2}$ +
spA=spSisestaArv(spA,17,4,1); # $T_{t4}$ -
spA=spSisestaArv(spA,17,25,-1); # $C_{25}$ summa on tasakaalus
# Sõlm 2
spA=spSisestaArv(spA,18,7,1); # $B_{7}$ - bimoment
spA=spSisestaArv(spA,18,11,1); # $B_{11}$ summa on tasakaalus
spA=spSisestaArv(spA,19,6,1); # $T_{t8}$ +
spA=spSisestaArv(spA,19,8,1); # $T_{w8}$ +
spA=spSisestaArv(spA,19,10,1); # $T_{t10}$ +
spA=spSisestaArv(spA,19,12,1); # $T_{w12}$ -
spA=spSisestaArv(spA,19,26,-1); # $-C_{26}$
# Sõlm 3
spA=spSisestaArv(spA,20,15,1); # $B_{15}$ - bimoment
spA=spSisestaArv(spA,20,19,1); # $B_{19}$ summa on tasakaalus
spA=spSisestaArv(spA,21,14,1); # $T_{t14}$ +
spA=spSisestaArv(spA,21,16,1); # $T_{w16}$ +
spA=spSisestaArv(spA,21,18,1); # $T_{t18}$ +
spA=spSisestaArv(spA,21,20,1); # $T_{w20}$ -
spA=spSisestaArv(spA,21,27,-1); # $C_{27}$ summa on tasakaalus
#SUM1=Z(25,1)+Z(26,1)+Z(27,1)
# Toetingimused
# Sõlm 1
spA=spSisestaArv(spA,22,1,1); # $theta_A$ - väändenurk on null
spA=spSisestaArv(spA,23,2,1); # $T_tA$ - kooldeväändemoment
# Sõlm 2
spA=spSisestaArv(spA,24,9,1); # $theta_A$ - väändenurk on null
# Sõlm 3
spA=spSisestaArv(spA,25,17,1); # $theta_A$ - väändenurk on null
# Sõlm 4
spA=spSisestaArv(spA,26,23,1); # $B_{L}$ - bimoment
Bvb(26,1)=By ;
spA=spSisestaArv(spA,27,22,1); # $T_{tL}+
spA=spSisestaArv(spA,27,24,1); # T_{\omega L}$ = üldväändemoment
#Bvb(27,1)=0.0;
#vastavad vabaliikmed Bvb on juba nullitud
#
#spA_rank = sprank(spA) # võrrandisüsteemi astak
Toereaktsioonid (toemomendid) leiab arvutuspäeviku väljavõttest 3.1.
Toereaktsioonid (toemomendid) C25 = -4.1206e+05 C26 = -5.8028e+05 C27 = -1.2767e+05
Algparameetrite arvutus.
Rajaväärtuste leidmisel korrutati väändenurgad skaleerimisteguriga:
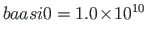 . Skaleerimata algparameetrite saamiseks tuleb vastavad suurused jagada skaleerimisteguriga. Talade 1, 2 ja 3 skaleerimata algparameetrid
on toodud arvutuspäeviku väljavõttes 3.2.
. Skaleerimata algparameetrite saamiseks tuleb vastavad suurused jagada skaleerimisteguriga. Talade 1, 2 ja 3 skaleerimata algparameetrid
on toodud arvutuspäeviku väljavõttes 3.2.
Algparameetrid - AP1 AP2 AP3
theta - 0.0000e+00 0.0000e+00 0.0000e+00
Tt - 0.0000e+00 4.7899e+04 3.4901e+04
B - 3.7593e+07 2.7948e+07 8.5483e+06
Tw - -4.1206e+05 -2.4023e+05 -3.4901e+04
Väändenurkade ja väändemomentide arvutus.
Väändenurkade ja väändemomentide leidmiseks tala ristlõigetes
kasutame ülekandevõrrandit (C.1)
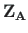 on tala algparameetrid (vt arvutuspäeviku väljavõte 3.2). Ülekandemaatriksi
on tala algparameetrid (vt arvutuspäeviku väljavõte 3.2). Ülekandemaatriksi
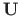 leiame GNU Octave'i funktsiooniga ylWGfhlin.m ning
koormusvektori
leiame GNU Octave'i funktsiooniga ylWGfhlin.m ning
koormusvektori
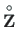 funktsioonidega yzWGmx.m
ja yzWGMx.m (vt väljavõte programmist 3.3).
funktsioonidega yzWGmx.m
ja yzWGMx.m (vt väljavõte programmist 3.3).
AP=AP1; baasi0=1.0 Nmitmeks=4 xx=0.0; xsamm=0.0; xsamm=l1/Nmitmeks; for ij=1:Nmitmeks+1 # 5 - displacements and forces at x=0.0 Xloikes(ij,1)=xx; vvF=ylWGfhlin(baasi0,l1,xx,GIt,EIw); vvB1=yzWGmx(baasi0,l1,xx,a1,mx1,GIt,EIw); Fvv(1:4,ij)=vvF*AP+vvB1; Fvv(5,ij)=Fvv(2,ij)+Fvv(4,ij); xx=xx+xsamm; endfor AP=AP2; baasi0=1.0 Nmitmeks=4 xx=0.0; xsamm=0.0; xsamm=l2/Nmitmeks; for ij=1:Nmitmeks+1 # 5 - displacements and forces at x=0.0 Xloikes(ij,1)=xx; vvF=ylWGfhlin(baasi0,l2,xx,GIt,EIw); vvB2=yzWGMx(baasi0,l2,xx,a2,Mx2,GIt,EIw); Fvv(1:4,ij)=vvF*AP+vvB2; Fvv(5,ij)=Fvv(2,ij)+Fvv(4,ij); xx=xx+xsamm; endfor AP=AP3; baasi0=1.0 Nmitmeks=4 xx=0.0; xsamm=0.0; xsamm=l3/Nmitmeks; for ij=1:Nmitmeks+1 # 5 - displacements and forces at x=0.0 Xloikes(ij,1)=xx; vvF=ylWGfhlin(baasi0,l3,xx,GIt,EIw); Fvv(1:4,ij)=vvF*AP; %+vvB3; Fvv(5,ij)=Fvv(2,ij)+Fvv(4,ij); xx=xx+xsamm; endfor
Arvutustulemused on esitatud arvutuspäeviku väljavõttes 3.3.
baasi0 = 1
Nmitmeks = 4
k = 0.0074270
x= 0.00 200.00 400.00 600.00 800.00
theta - 0.000e+00 1.267e-02 2.194e-02 1.442e-02 -2.665e-15
Tt - 0.000e+00 1.225e+05 8.375e+03 -1.155e+05 -4.790e+04
B - -3.759e+07 5.007e+06 1.292e+07 7.084e+06 -2.795e+07
Tw - 4.121e+05 8.954e+04 3.682e+03 -7.244e+04 -3.400e+05
Tsum - 4.121e+05 2.121e+05 1.206e+04 -1.879e+05 -3.879e+05
baasi0 = 1
Nmitmeks = 4
k = 0.0074270
x= 0.00 150.00 300.00 450.00 600.00
theta - 0.000e+00 2.621e-03 8.051e-03 5.148e-03 -1.665e-16
Tt - -4.790e+04 6.909e+04 1.663e+04 -5.742e+04 -3.490e+04
B - -2.795e+07 -3.196e+06 1.716e+07 2.552e+06 -8.548e+06
Tw - 2.402e+05 1.232e+05 -1.443e+05 -7.024e+04 -9.277e+04
Tsum - 1.923e+05 1.923e+05 -1.277e+05 -1.277e+05 -1.277e+05
x = 299.9999999999
theta - 8.051e-03
Tt - 1.663e+04
B - 1.716e+07
Tw - 1.757e+05
Tsum - 1.923e+05
baasi0 = 1
Nmitmeks = 4
k = 0.0074270
x= 0.00 50.00 100.00 150.00 200.00
theta - 0.000e+00 -7.605e-04 -8.646e-04 -3.266e-04 9.283e-04
Tt - -3.490e+04 -1.321e+04 6.632e+03 2.740e+04 5.199e+04
B - -8.548e+06 -7.359e+06 -7.196e+06 -8.038e+06 -1.000e+07
Tw - 3.490e+04 1.321e+04 -6.632e+03 -2.740e+04 -5.199e+04
Tsum - 0.000e+00 0.000e+00 0.000e+00 0.000e+00 7.276e-12
Leitud tulemuste põhjal koostame jätuvtala epüürid (jn 3.6).
EST-meetodiga saadud tulemused on kooskõlas raamatus [Bõt62] jõu- ja deformatsioonimeetodi abil leitutega (vt tabelid 3.1, 3.2 ja 3.3).
| x [cm] | Z(x) | [Bõt62] | Mõõtühik | EST-meetod | Mõõtühik |
| 0.0 | θ | rad | 0.000×100 | rad | |
| Tt | kG·m | 0.000×100 | N·cm | ||
| Bω | –3.762×102 | kG·m2 | –3.759×107 | N·cm2 | |
| Tω | kG·m | 4.121×105 | N·cm | ||
| Tsum | 4.120×102 | kG·m | 4.121×105 | N·cm | |
| 200 | θ | rad | 1.267×10-2 | rad | |
| Tt | kG·m | 1.225×105 | N·cm | ||
| Bω | 4.89×101 | kG·m2 | 5.007×106 | N·cm2 | |
| Tω | kG·m | 8.954×104 | N·cm | ||
| Tsum | kG·m | 2.121×105 | N·cm | ||
| 400 | θ | rad | 2.194×10-2 | rad | |
| Tt | kG·m | 8.375×103 | N·cm | ||
| Bω | 1.292×102 | kG·m2 | 1.292×107 | N·cm2 | |
| Tω | kG·m | 3.682×103 | N·cm | ||
| Tsum | kG·m | 1.206×104 | N·cm | ||
| 600 | θ | rad | 1.442×10-2 | rad | |
| Tt | kG·m | –1.155×105 | N·cm | ||
| Bω | 7.000×101 | kG·m2 | 7.084×106 | N·cm2 | |
| Tω | kG·m | –7.244×104 | N·cm | ||
| Tsum | kG·m | –1.879×105 | N·cm | ||
| 800 | θ | rad | –2.665×10-15 | rad | |
| Tt | kG·m | –4.790×104 | N·cm | ||
| Bω | –2.794×102 | kG·m2 | –2.795×107 | N·cm2 | |
| Tω | kG·m | –3.400×105 | N·cm | ||
| Tsum | –3.880×102 | kG·m | –3.879×105 | N·cm | |
| 0.0 | θ | rad | 0.000×100 | rad | |
| Tt | kG·m | –4.790×104 | N·cm | ||
| Bω | –2.794×102 | kG·m2 | –2.795×107 | N·cm2 | |
| Tω | kG·m | 2.402×105 | N·cm | ||
| Tsum | 1.920×102 | kG·m | 1.923×105 | N·cm |
| x [cm] | Z(x) | [Bõt62] | Mõõtühik | EST-meetod | Mõõtühik |
| 150 | θ | rad | 2.621×10-3 | rad | |
| Tt | kG·m | 6.909×104 | N·cm | ||
| Bω | –3.20×101 | kG·m2 | –3.196×106 | N·cm2 | |
| Tω | kG·m | 1.232×105 | N·cm | ||
| Tsum | 1.920×102 | kG·m | 1.923×105 | N·cm | |
| 300 | θ | rad | 8.051×10-3 | rad | |
| Tt | kG·m | 1.663×104 | N·cm | ||
| Bω | 1.722×102 | kG·m2 | 1.716×107 | N·cm2 | |
| Tω | kG·m | –1.443×105 | N·cm | ||
| 300 – ε | Tsum | 1.920×102 | kG·m | 1.923×105 | N·cm |
| 300 | Tsum | –1.280×102 | kG·m | –1.277×105 | N·cm |
| 300 | θ | rad | 5.148×10-3 | rad | |
| Tt | kG·m | –5.742×104 | N·cm | ||
| Bω | 2.56×101 | kG·m2 | 2.552×106 | N·cm2 | |
| Tω | kG·m | –7.024×104 | N·cm | ||
| Tsum | –1.280×102 | kG·m | –1.277×105 | N·cm | |
| 450 | θ | rad | –1.665×10-16 | rad | |
| Tt | kG·m | –3.490×104 | N·cm | ||
| Bω | –8.54×101 | kG·m2 | –8.548×106 | N·cm2 | |
| Tω | kG·m | –9.277×104 | N·cm | ||
| Tsum | –1.280×102 | kG·m | –1.277×105 | N·cm | |
| 600 | θ | rad | 0.000 | rad | |
| Tt | kG·m | –3.490×104 | N·cm | ||
| Bω | –8.54×101 | kG·m2 | –8.548×106 | N·cm2 | |
| Tω | kG·m | 3.490×104 | N·cm | ||
| Tsum | 0.00 | kG·m | 0.000×100 | N·cm | |
| 0.0 | θ | rad | –8.646×10-4 | rad | |
| Tt | kG·m | 6.632×103 | N·cm | ||
| Bω | –7.17×101 | kG·m2 | –7.196×106 | N·cm2 | |
| Tω | kG·m | –6.632×103 | N·cm | ||
| Tsum | 0.00 | kG·m | 0.000×100 | N·cm |
| x [cm] | Z(x) | [Bõt62] | Mõõtühik | EST-meetod | Mõõtühik |
| 100 | θ | rad | –8.646×10-4 | rad | |
| Tt | kG·m | 6.632×103 | N·cm | ||
| Bω | –7.17×101 | kG·m2 | –7.196×106 | N·cm2 | |
| Tω | kG·m | –6.632×103 | N·cm | ||
| Tsum | 0.00 | kG·m | 0.000×100 | N·cm | |
| 200 | θ | rad | 9.283×10-4 | rad | |
| Tt | kG·m | 5.199×104 | N·cm | ||
| Bω | –1.000×102 | kG·m2 | –1.000×107 | N·cm2 | |
| Tω | kG·m | –5.199×104 | N·cm | ||
| Tsum | 0.00 | kG·m | 7.276×10-12 | N·cm |
Joonisel 3.7 on hõreda maatriksi muster (hõreda maatriksi spA(27,27) nullist erinevate elementide asukohad).
andres