Järgmine: C.1 Koormusvektorid Üles: Lisad Eelmine: B.2 Varrassüsteemi rajaülesanne
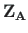 ,
,
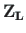 on vastavalt varda alguses ja lõpus olevad siirded, paindenurgad, põikjõud, paindemomendid, väändenurgad ja väändemomendid.
on vastavalt varda alguses ja lõpus olevad siirded, paindenurgad, põikjõud, paindemomendid, väändenurgad ja väändemomendid.
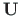 teise märgikokkuleppe puhul on
teise märgikokkuleppe puhul on
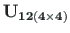 kirjeldab tala painet (vt [Lah12Lah12, lk 688]6.1):
kirjeldab tala painet (vt [Lah12Lah12, lk 688]6.1):
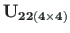 õhukeseseinalise tala takistatud väänet:
õhukeseseinalise tala takistatud väänet:
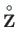 on tala koormusvektor,
mis koosneb painde koormusvektorist
on tala koormusvektor,
mis koosneb painde koormusvektorist
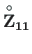 ja takistatud väände koormusvektorist
ja takistatud väände koormusvektorist
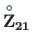 :
:
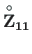 (vt [Lah12, avaldis (1.66) 6.2ja tabel G.1 6.3)] saab
siirde
(vt [Lah12, avaldis (1.66) 6.2ja tabel G.1 6.3)] saab
siirde 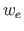 erilahendite tuletistest:
erilahendite tuletistest:
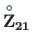 saab
väändenurga
saab
väändenurga
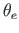 erilahendite tuletistest:
erilahendite tuletistest:
Koormusvektori
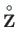 valime tabelitest
C.1 ja C.2.
valime tabelitest
C.1 ja C.2.
Õhukeseseinalise tala painde ja takistatud väände ülekandevõrrandid võib kirjutada võrrandisüsteemina
Lühemalt
kus
kus