Järgmine: 3.1.3 Murtud teljega -tala Üles: 3.1 Rajatingimused Eelmine: 3.1.1 Jätkuvtala arvutus
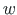 , paindenurga
, paindenurga
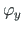 , põikjõu
, põikjõu 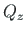 ,
paindemomendi
,
paindemomendi 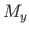 ,
väändenurga
,
väändenurga
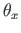 , vabaväändemomendi
, vabaväändemomendi 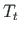 , bimomendi
, bimomendi
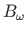 ja
kooldeväändemomendi
ja
kooldeväändemomendi
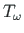 epüürid.
epüürid.
Andmed. Murtud teljega tala elementide pikkused
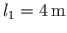 ja
ja
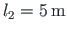 . Teine ava on ekstsentriliselt koormatud ühtlase lauskoormusega
. Teine ava on ekstsentriliselt koormatud ühtlase lauskoormusega
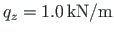 . Vertikaalse lauskoormuse
. Vertikaalse lauskoormuse 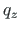 ekstsentrilisus
ekstsentrilisus
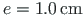 .
Ristlõikeks on valitud I-profiil nr 60a [Bõt62, lk 435].
Ristlõike paindejäikus
.
Ristlõikeks on valitud I-profiil nr 60a [Bõt62, lk 435].
Ristlõike paindejäikus
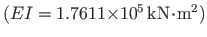 ,
kooldejäikus
,
kooldejäikus
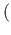
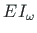
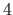 ,
vabaväändejäikus
,
vabaväändejäikus
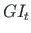
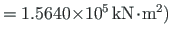 ning
kooldekarakteristik
ning
kooldekarakteristik
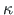
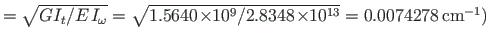 on konstantsed.
on konstantsed.
Lahendus. Kanname ühtlaselt jaotatud põikkoormuse 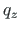 elastsele teljele (jn 1.21 ja tabel 1.1). Vaatleme kahte koormusjuhtu (jn 3.9), kus elastsel teljel on ühtlaselt jaotatud väändemoment
elastsele teljele (jn 1.21 ja tabel 1.1). Vaatleme kahte koormusjuhtu (jn 3.9), kus elastsel teljel on ühtlaselt jaotatud väändemoment
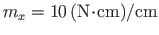 ja ühtlaselt jaotatud põikkoormus
ja ühtlaselt jaotatud põikkoormus
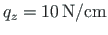 .
.
Rajaväärtuste arvutamiseks kasutame nagu EST-meetodi [Lah97a], [Lah14]
puhulgi hõredat võrrandisüsteemi 3.13
 on võrrandisüsteemi
tundmatute vektor
on võrrandisüsteemi
tundmatute vektor
 ja
ja  alguses ning lõpus:
alguses ning lõpus:
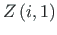 indeks (i=1, 2, 3,
indeks (i=1, 2, 3,  , 32) on toodud joonisel 3.9.
, 32) on toodud joonisel 3.9.
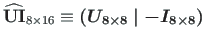 (C.13)
arvutamiseks saab kasutada GNU Octave'i funktsioone yspTVmI.m ja yspTVlin.m.
(C.13)
arvutamiseks saab kasutada GNU Octave'i funktsioone yspTVmI.m ja yspTVlin.m.
Võrrandisüsteemis (3.20) on tundmatuid poole rohkem kui võrrandeid. Kanname need võrrandid võrrandisüsteemi (3.16) (vt väljavõte programmist 3.4).
# Esimese tala hõreda laiendatud ülekandemaatriksi arvutus
spvF=yspTVmI(baasi0,l1,l1,GAr,EI,GIt,EIw);
IIv=1;
IJv=1;
# sisestab ülekandemaatriksi võrrandisüsteemi spA*Z=Bvb
spA=spInsertBtoA(spA,IIv,IJv,spvF);
# võrrandisüsteemi vabaliige Bvb on eelnevalt nullitud
# Teise tala hõreda laiendatud ülekandemaatriksi arvutus
spvF=yspTVmI(baasi0,l2,l2,GAr,EI,GIt,EIw);
#vB2a=yzTVqz(baasi0,l2,0.0,qz,EI) # koormusvektori arvutus
vB2b=yzTVmx(baasi0,l2,l2,0.0,mx,GIt,EIw) # koormusvektori arvutus
#vB2=vB2a+vB2b
vB2=vB2b
krda=2;
IIv=krda*8-7;
IJv=krda*16-15;
# sisestab ülekandemaatriksi võrrandisüsteemi spA*Z=Bvb
spA=spInsertBtoA(spA,IIv,IJv,spvF);
# sisestab koormusvektori võrrandisüsteemi vabaliikmesse Bvb
Bvb=InsertBtoA(Bvb,NNK,1,IIv,1,vB2,8,1);
Võrrandisüsteemis (3.16) peab olema võrrandeid ja tundmatuid ühepalju. Võrrandite arv
peab ühtima maatriksi
 astakuga. Puuduvad sõltumatud võrrandid saame
kinemaatilistest ja staatilistest rajatingimustest.
Varrassüsteemi elemente ühendavad sidemed võib jagada välis- ja sisesidemeteks [Jür85, lk 8-9].
3.15 Reaktsioonid jagatakse
välimisteks ja sisemisteks. 3.16 Sisemiste reaktsioonide summa võrdub nulliga. Vaadeldes varrassüsteemi kui tervikut, võime
sisemisi reaktsioone nimetada ka kontaktjõududeks. 3.17
astakuga. Puuduvad sõltumatud võrrandid saame
kinemaatilistest ja staatilistest rajatingimustest.
Varrassüsteemi elemente ühendavad sidemed võib jagada välis- ja sisesidemeteks [Jür85, lk 8-9].
3.15 Reaktsioonid jagatakse
välimisteks ja sisemisteks. 3.16 Sisemiste reaktsioonide summa võrdub nulliga. Vaadeldes varrassüsteemi kui tervikut, võime
sisemisi reaktsioone nimetada ka kontaktjõududeks. 3.17
Sisemised kinemaatilised ja staatilised rajatingimused: 3.18
Järgnevalt
Rajatingimuste püstitus. Väliste rajatingimuste seadmisel tuleb arvestada energiateoreemi 3.19 (B.8).
Kui avaldistes
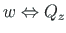 ,
,
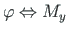 ,
,
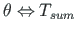 ,
,
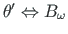 üks pool (siire
üks pool (siire 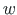 , paindenurk
, paindenurk 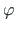 , pöördenurk
, pöördenurk 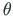 , suhteline väändenurk
, suhteline väändenurk
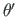 ) on antud, siis teine pool (põikjõud
) on antud, siis teine pool (põikjõud 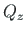 , paindemoment
, paindemoment 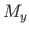 , koguväändemoment
, koguväändemoment 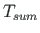 , bimoment
, bimoment
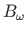 ) on tundmatu.
) on tundmatu.
Talal on sõlmedes  ja
ja 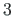 jäigad toed, mis ei võimalda pööret ega kooldumist (vt tabel 1.2).
jäigad toed, mis ei võimalda pööret ega kooldumist (vt tabel 1.2).
Sisemistest rajatingimustest vaatleme sõlmes 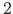 pidevustingimusi.
Varraste
pidevustingimusi.
Varraste 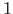 ja
ja 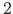 siirded ja kooldumus 3.20 on võrdsed.
siirded ja kooldumus 3.20 on võrdsed.
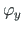 ,
,
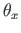 ) puhul peame arvestama, et varda x-telg on murtud (telgede pööre nurga
) puhul peame arvestama, et varda x-telg on murtud (telgede pööre nurga 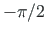 võrra ümber z-telje, vt avaldis (D.17)).
võrra ümber z-telje, vt avaldis (D.17)).
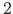 tasakaalutingimusi. Painde- ja väändemomentide
(
tasakaalutingimusi. Painde- ja väändemomentide
(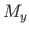 ja
ja
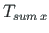 ) puhul peame arvestama, et varda x-telg on murtud (telgede pööre nurga
) puhul peame arvestama, et varda x-telg on murtud (telgede pööre nurga 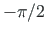 võrra ümber z-telje vt avaldis (D.17)).
võrra ümber z-telje vt avaldis (D.17)).
Koostatud on 16 rajatingimuse võrrandit. Sisestame need võrrandisüsteemi (3.16) (vt väljavõte programmist 3.5). Võrrandisüsteemi astak võrdub tundmatute arvuga. Järelikult on sisestatud võrrandid lineaarselt sõltumatud.
########## Rajatingimused
# sõlm 1
spA=spSisestaArv(spA,17,1,1); # siire w
spA=spSisestaArv(spA,18,2,1); # pööre fi
spA=spSisestaArv(spA,19,5,1); # $theta$ - väändenurk
spA=spSisestaArv(spA,20,6,1); # $T_t$ ($theta^{\prime}$)
# sõlm 2
# pidevus
spA=spSisestaArv(spA,21,9,1); # siire w
spA=spSisestaArv(spA,21,17,-1);
spA=spSisestaArv(spA,22,10,1); # pööre fi
spA=spSisestaArv(spA,22,21,1);
spA=spSisestaArv(spA,23,13,1); # väändenurk
spA=spSisestaArv(spA,23,18,-1);
spA=spSisestaArv(spA,24,14,1);
spA=spSisestaArv(spA,24,22,1);
# tasakaal
spA=spSisestaArv(spA,25,11,1); # Q
spA=spSisestaArv(spA,25,19,1);
spA=spSisestaArv(spA,26,12,-1); # M
spA=spSisestaArv(spA,26,22,1); # $T_t$
spA=spSisestaArv(spA,26,24,1); # $T_{\omega}$
spA=spSisestaArv(spA,27,20,1); # M
spA=spSisestaArv(spA,27,14,1); # $T_t$
spA=spSisestaArv(spA,27,16,1); # $T_{\omega}$
spA=spSisestaArv(spA,28,15,1); # B
spA=spSisestaArv(spA,28,23,1);
# sõlm 3
spA=spSisestaArv(spA,29,25,1); # siire w
spA=spSisestaArv(spA,30,26,-1); # pööre fi
spA=spSisestaArv(spA,31,29,1); # $theta$ - väändenurk
spA=spSisestaArv(spA,32,30,1); # $T_t$ ($theta^{\prime}$)
#
spA_rank = sprank(spA) # võrrandisüsteemi astak
Pärast põhivõrrandite sisestamist on võrrandisüsteemis spA_rida = 16 spA_veergu = 32 Pärast toel 1 toetingimuste lisamist on võrrandisüsteemis spA_rida = 20 spA_veergu = 32 Pärast pidevusvõrrandite lisamist on võrrandisüsteemis spA_rida = 24 spA_veergu = 32 Pärast tasakaaluvõrrandite lisamist on võrrandisüsteemis spA_rida = 28 spA_veergu = 32 Pärast toel 3 toetingimuste lisamist on võrrandisüsteemis spA_rida = 32 spA_veergu = 32 spA_rank = 32
Algparameetrite arvutus.
Rajaväärtuste leidmisel korrutasime siirded, paindenurgad ja väändenurgad skaleerimisteguriga:
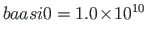 . Skaleerimata algparameetrite saamiseks
tuleb vastavad suurused jagada skaleerimisteguriga. Talade 1 ja 2 skaleerimata algparameetrid
on toodud arvutuspäeviku väljavõttes 3.5.
. Skaleerimata algparameetrite saamiseks
tuleb vastavad suurused jagada skaleerimisteguriga. Talade 1 ja 2 skaleerimata algparameetrid
on toodud arvutuspäeviku väljavõttes 3.5.
Algparameetrid - AP1 ja AP2
w - 0.0000e+00 7.6081e-05
fi - 0.0000e+00 2.4997e-07
Q - 2.2973e+00 2.2973e+00
M - 1.3685e+03 3.0610e+02
theta - 0.0000e+00 4.1519e-07
Tt - 0.0000e+00 -3.9865e+02
B - -3.1677e+04 9.1154e+04
Tw - 3.0610e+02 -1.8888e+03
3. Siirete, nurkade ja momentide arvutus.
Siirete, painde- ja väändenurkade, põikjõudude, painde- ja väändemomentide leidmiseks tala ristlõigetes
kasutame ülekandevõrrandit (C.1)
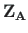 on tala algparameetrid (vt arvutuspäeviku väljavõte 3.5). Ülekandemaatriksi
on tala algparameetrid (vt arvutuspäeviku väljavõte 3.5). Ülekandemaatriksi
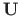 leiame GNU Octave'i funktsiooniga ylTVlin.m
ning koormusvektori
leiame GNU Octave'i funktsiooniga ylTVlin.m
ning koormusvektori
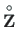 funktsioonidega yzTVmx.m
ja yzTVqz.m (vt väljavõte programmist 3.6).
funktsioonidega yzTVmx.m
ja yzTVqz.m (vt väljavõte programmist 3.6).
AP=AP1; for ij=1:Nmitmeks+1 # 5 - displacements and forces at x=0.0 Xloikes(ij,1)=xx; vvF=ylTVlin(baasi0,l1,xx,GAr,EI,GIt,EIw); Fvv(1:8,ij)=vvF*AP; %%+vvB1; Fvv(9,ij)=Fvv(6,ij)+Fvv(8,ij); xx=xx+xsamm; endfor AP=AP2; for ij=1:Nmitmeks+1 # 5 - displacements and forces at x=0.0 Xloikes(ij,1)=xx; vvF=ylTVlin(baasi0,l2,xx,GAr,EI,GIt,EIw); vB2b=yzTVmx(baasi0,l2,xx,0.0,mx,GIt,EIw); vB2=vB2b; Fvv(1:8,ij)=vvF*AP+vB2; Fvv(9,ij)=Fvv(6,ij)+Fvv(8,ij); xx=xx+xsamm; endfor
Arvutustulemused on esitatud arvutuspäeviku väljavõttes 3.6.
baasi0 = 1
Nmitmeks = 4
k = 0.0074270
x= 0.00 100.00 200.00 300.00 400.00
w - 0.000e+00 4.103e-06 1.728e-05 4.084e-05 7.608e-05
fi - 0.000e+00 -8.423e-08 -1.815e-07 -2.918e-07 -4.152e-07
Q - -2.297e+00 -2.297e+00 -2.297e+00 -2.297e+00 -2.297e+00
M - -1.368e+03 -1.598e+03 -1.828e+03 -2.058e+03 -2.287e+03
theta - 0.000e+00 -3.999e-06 -1.070e-05 -1.267e-05 2.500e-07
Tt - 0.000e+00 -1.029e+02 -8.839e+01 5.180e+01 3.987e+02
B - 3.168e+04 7.320e+03 -1.281e+04 -4.034e+04 -9.115e+04
Tw - -3.061e+02 -2.032e+02 -2.177e+02 -3.579e+02 -7.048e+02
Tsum - -3.061e+02 -3.061e+02 -3.061e+02 -3.061e+02 -3.061e+02
baasi0 = 1
Nmitmeks = 4
k = 0.0074270
x= 0.00 125.00 250.00 375.00 500.00
w - 7.608e-05 4.662e-05 2.242e-05 6.029e-06 1.355e-20
fi - 2.500e-07 2.181e-07 1.658e-07 9.307e-08 -6.617e-23
Q - -2.297e+00 -2.297e+00 -2.297e+00 -2.297e+00 -2.297e+00
M - -3.061e+02 -5.933e+02 -8.804e+02 -1.168e+03 -1.455e+03
theta - 4.152e-07 4.031e-05 5.547e-05 2.942e-05 2.168e-19
Tt - 3.987e+02 4.348e+02 -8.698e+01 -4.925e+02 0.000e+00
B - -9.115e+04 5.426e+04 8.211e+04 1.816e+04 -1.968e+05
Tw - 1.889e+03 6.027e+02 -1.256e+02 -9.701e+02 -2.713e+03
Tsum - 2.287e+03 1.037e+03 -2.126e+02 -1.463e+03 -2.713e+03
Leitud tulemuste põhjal koostame L-tala epüürid koormusest 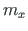 (jn 3.10, b-j).
(jn 3.10, b-j).
— — —
EST-meetodiga saadud tulemused on kooskõlas raamatus [Bõt62] jõu- ja deformatsioonimeetodi
abil leitutega
(vt tabelid 3.4 ja 3.5).
| x [ cm] | Z(x) | Jõumeetod [Bõt62] |
Def-meetod [Bõt62] |
Mõõtühik | EST-meetod | Mõõtühik |
| 0.0 | w | m | 0.000 | cm | ||
| φ | rad | 0.000 | rad | |||
| Qz | kG | –2.297 | N | |||
| My | –1.38×102 | –1.34×102 | kG·m | –1.368×103 | N·cm | |
| θ | rad | 0.000 | rad | |||
| Tt | kG·m | 0.000 | N·cm | |||
| Bω | 3.22×103 | 3.21×103 | kG·m2 | 3.168×104 | N·cm2 | |
| Tω | kG·m | –3.061×102 | N·cm | |||
| Tsum | kG·m | –3.061×102 | N·cm | |||
| 200 | w | m | 1.728×10–5 | cm | ||
| φ | rad | –1.815×10–7 | rad | |||
| Qz | kG | –2.297 | N | |||
| My | kG·m | –1.828×103 | N·cm | |||
| θ | rad | –1.070×10–5 | rad | |||
| Tt | kG·m | –8.839×101 | N·cm | |||
| Bω | kG·m2 | –1.281×104 | N·cm2 | |||
| Tω | kG·m | –1.281×104 | N·cm | |||
| Tsum | kG·m | –3.061×102 | N·cm | |||
| 400 – ε | w | m | 7.608×10–5 | cm | ||
| φ | rad | –4.152×10–7 | rad | |||
| Qz | kG | –2.297 | N | |||
| My | –2.30×102 | 2.28×102 3.21 | kG·m | –2.287×103 | N·cm | |
| θ | rad | 2.500×10–7 | rad | |||
| Tt | kG·m | 3.987×102 | N·cm | |||
| Bω | –9.20×103 | 9.18×103 | kG·m2 | –9.115×104 | N·cm2 | |
| Tω | kG·m | –7.048×102 | N·cm | |||
| Tsum | kG·m | –3.061×102 | N·cm |
| x [ cm] | Z(x) | Jõumeetod [Btõ;62] |
Def-meetod [Btõ62] |
Mõõtühik | EST-meetod | Mõõtühik |
| 400 + ε | w | m | 7.608×10–5 | cm | ||
| φ | rad | 2.500×10–7 | rad | |||
| Qz | kG | –2.297×100 | N | |||
| My | –3.11×101 | –2.92×101 | kG·m | –3.061×102 | N·cm | |
| θ | rad | 4.152×10–7 | rad | |||
| Tt | kG·m | 3.987×102 | N·cm | |||
| Bω | –9.20×103 | –9.13×103 | kG·m2 | –9.115×104 | N·cm2 | |
| Tω | kG·m | 1.889×103 | N·cm | |||
| Tsum | kG·m | 2.287×103 | N·cm | |||
| 650 | w | m | 2.242×10–5 | cm | ||
| φ | rad | 1.658×10–7 | rad | |||
| Qz | kG | –2.297×100 | N | |||
| My | kG·m | –8.804×102 | N·cm | |||
| θ | rad | 5.547×10–5 | rad | |||
| Tt | kG·m | –8.698×101 | N·cm | |||
| Bω | kG·m2 | 8.211×104 | N·cm2 | |||
| Tω | kG·m | –1.256×102 | N·cm | |||
| Tsum | kG·m | –2.126×102 | N·cm | |||
| 900 | w | m | 1.355e-20 | cm | ||
| φ | rad | –6.617e-23 | rad | |||
| Qz | kG | –2.297×100 | N | |||
| My | –1.47×102 | 1.44×102 | kG·m | –1.455×103 | N·cm | |
| θ | rad | 2.168e-19 | rad | |||
| Tt | kG·m | 0.000 | N·cm | |||
| Bω | –1.97×104 | 1.97×104 | kG·m2 | –1.968×105 | N·cm2 | |
| Tω | kG·m | –2.713×103 | N·cm | |||
| Tsum | kG·m | –2.713×103 | N·cm |
Joonisel 3.11 on hõreda maatriksi muster (hõreda maatriksi spA(32,32) nullist erinevate elementide asukohad).
Edasi arvutame GNU Octave'i programmiga Naide4_5GammaTV.m
sedasama murtud teljega tala, kui tala teine ava on koormatud ühtlase lauskoormusega
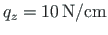 .
Programm erineb eelnevast ainult koormusvektori poolest (vt väljavõte programmist 3.7).
.
Programm erineb eelnevast ainult koormusvektori poolest (vt väljavõte programmist 3.7).
# Esimese tala hõreda laiendatud ülekandemaatriksi arvutus
spvF=yspTVmI(baasi0,l1,l1,GAr,EI,GIt,EIw);
IIv=1;
IJv=1;
# sisestab ülekandemaatriksi võrrandisüsteemi spA*Z=Bvb
spA=spInsertBtoA(spA,IIv,IJv,spvF);
# võrrandisüsteemi vabaliige Bvb on eelnevalt nullitud
# Teise tala hõreda laiendatud ülekandemaatriksi arvutus
spvF=yspTVmI(baasi0,l2,l2,GAr,EI,GIt,EIw);
vB2a=yzTVqz(baasi0,l2,0.0,qz,EI) # koormusvektori arvutus
#vB2b=yzTVmx(baasi0,l2,l2,0.0,mx,GIt,EIw) # koormusvektori arvutus
#vB2=vB2a+vB2b
vB2=vB2a
IIv=krda*8-7;
IJv=krda*16-15;
# sisestab ülekandemaatriksi võrrandisüsteemi spA*Z=Bvb
spA=spInsertBtoA(spA,IIv,IJv,spvF);
# sisestab koormusvektori võrrandisüsteemi vabaliikmesse Bvb
Bvb=InsertBtoA(Bvb,NNK,1,IIv,1,vB2,8,1);
Sisestatud võrrandite arvu ja astakut saab kontrollida arvutuspäeviku väljavõttest 3.7.
Pärast põhivõrrandite sisestamist on võrrandisüsteemis spA_rida = 16 spA_veergu = 32 Pärast toel 1 toetingimuste lisamist on võrrandisüsteemis spA_rida = 20 spA_veergu = 32 Pärast pidevusvõrrandite lisamist on võrrandisüsteemis spA_rida = 24 spA_veergu = 32 Pärast tasakaaluvõrrandite lisamist on võrrandisüsteemis spA_rida = 28 spA_veergu = 32 Pärast toel 3 toetingimuste lisamist on võrrandisüsteemis spA_rida = 32 spA_veergu = 32 spA_rank = 32
Talade 1 ja 2 skaleerimata algparameetrid on toodud arvutuspäeviku väljavõttes 3.8.
Algparameetrid - AP1 ja AP2
w - 0.0000e+00 1.5004e-02
fi - 0.0000e+00 3.0202e-05
Q - -1.2399e+03 -1.2399e+03
M - 4.9561e+05 -3.1834e+02
theta - 0.0000e+00 5.6245e-05
Tt - 0.0000e+00 2.2587e+01
B - 3.8369e+04 -4.1739e+04
Tw - -3.1834e+02 3.2666e+02
Arvutustulemused on esitatud arvutuspäeviku väljavõttes 3.9.
baasi0 = 1
Nmitmeks = 4
k = 0.0074270
x= 0.00 100.00 200.00 300.00 400.00
w - 0.000e+00 1.290e-03 4.690e-03 9.496e-03 1.500e-02
fi - 0.000e+00 -2.462e-05 -4.220e-05 -5.274e-05 -5.625e-05
Q - 1.240e+03 1.240e+03 1.240e+03 1.240e+03 1.240e+03
M - -4.956e+05 -3.716e+05 -2.476e+05 -1.236e+05 3.492e+02
theta - 0.000e+00 5.161e-06 1.571e-05 2.600e-05 3.020e-05
Tt - 0.000e+00 1.397e+02 1.764e+02 1.310e+02 -2.259e+01
B - -3.837e+04 -1.461e+04 7.258e+02 1.648e+04 4.174e+04
Tw - 3.183e+02 1.786e+02 1.420e+02 1.874e+02 3.409e+02
Tsum - 3.183e+02 3.183e+02 3.183e+02 3.183e+02 3.183e+02
baasi0 = 1
Nmitmeks = 4
k = 0.0074270
x= 0.00 125.00 250.00 375.00 500.00
w - 1.500e-02 1.106e-02 6.539e-03 2.156e-03 1.735e-18
fi - 3.020e-05 3.388e-05 3.746e-05 2.987e-05 -1.355e-20
Q - 1.240e+03 -1.011e+01 -1.260e+03 -2.510e+03 -3.760e+03
M - 3.183e+02 7.718e+04 -2.209e+03 -2.378e+05 -6.297e+05
theta - 5.625e-05 4.600e-05 2.741e-05 9.112e-06 1.084e-19
Tt - -2.259e+01 -2.024e+02 -2.462e+02 -1.946e+02 9.095e-13
B - 4.174e+04 1.410e+04 -4.868e+02 -1.552e+04 -4.493e+04
Tw - -3.267e+02 -1.469e+02 -1.030e+02 -1.546e+02 -3.492e+02
Tsum - -3.492e+02 -3.492e+02 -3.492e+02 -3.492e+02 -3.492e+02
Leitud tulemuste põhjal koostame L-tala epüürid koormusest 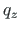 (jn 3.12, b-j).
(jn 3.12, b-j).
— — —
Tabelitest 3.6 ja 3.7 selgub, et EST-meetodiga saadud tulemused on kooskõlas raamatus [Bõt62] jõu- ja deformatsioonimeetodi abil leitutega.
| x [ cm] | Z(x) | Jõumeetod [Btš62] |
Def-meetod [Btš62] |
Mõõtühik | EST-meetod | Mõõtühik |
| 0.0 | w | m | 0.000×100 | cm | ||
| φ | rad | 0.000×100 | rad | |||
| Qz | kG | 1.240×103 | N | |||
| My | –4.96×104 | –4.93×104 | kG·m | –4.956×105 | N·cm | |
| θ | rad | 0.000×100 | rad | |||
| Tt | kG·m | 0.000×100 | N·cm | |||
| Bω | –3.82×103 | –3.79×103 | kG·m2 | –3.837×104 | N·cm2 | |
| Tω | kG·m | 3.183×102 | N·cm | |||
| Tsum | kG·m | 3.183×102 | N·cm | |||
| 200 | w | m | 4.690×10–3 | cm | ||
| φ | rad | –4.220×10–5 | rad | |||
| Qz | kG | 1.240×103 | N | |||
| My | kG·m | –2.476×105 | N·cm | |||
| θ | rad | 1.571×10–5 | rad | |||
| Tt | kG·m | 1.764×102 | N·cm | |||
| Bω | kG·m2 | 7.258×102 | N·cm2 | |||
| Tω | kG·m | 1.420×102 | N·cm | |||
| Tsum | kG·m | 3.183×102 | N·cm | |||
| 400 – ε | w | –1.49×10–2 | m | 1.500×10–2 | cm | |
| φ | rad | –5.625×10–5 | rad | |||
| Qz | kG | 1.240×103 | N | |||
| My | 3.46×101 | 2.2×101 3.22 | kG·m | 3.492×102 | N·cm | |
| θ | 2.98×10–5 | rad | 3.020×10–5 | rad | ||
| Tt | –1.49×10–8 3.23 | kG·m | –2.259×101 | N·cm | ||
| Bω | –4.14×103 | –4.14×103 | kG·m2 | 4.174×104 | N·cm2 | |
| Tω | kG·m | 3.409×102 | N·cm | |||
| Tsum | kG·m | 3.183×102 | N·cm |
| x [ cm] | Z(x) |
Jõumeetod [Btš62] |
Def-meetod [Btš62] |
Mõõtühik | EST-meetod | Mõõtühik |
| 400 + ε | w | –1.49×10–2 | m | 1.500×10–2 | cm | |
| φ | rad | 3.020×10–5 | rad | |||
| Qz | kG | 1.240×103 | N | |||
| My | 3.17×101 | 2.90×102 | kG·m | 3.183×102 | N·cm | |
| θ | –5.60×10–5 | rad | 5.625×10–5 | rad | ||
| Tt | –1.49×10–8 3.24 | kG·m | –2.259×101 | N·cm | ||
| Bω | 4.14×103 | 4.14×103 | kG·m2 | 4.174×104 | N·cm2 | |
| Tω | kG·m | –3.267×102 | N·cm | |||
| Tsum | kG·m | –3.492×102 | N·cm | |||
| 650 | w | m | 6.539×10–3 | cm | ||
| φ | rad | 3.746×10–5 | rad | |||
| Qz | kG | –1.260×103 | N | |||
| My | kG·m | –2.209×103 | N·cm | |||
| θ | rad | 2.741×10–5 | rad | |||
| Tt | kG·m | –2.462×102 | N·cm | |||
| Bω | kG·m2 | –4.868×102 | N·cm2 | |||
| Tω | kG·m | –1.030×102 | N·cm | |||
| Tsum | kG·m | –3.492×102 | N·cm | |||
| 900 | w | m | 1.735×10–18 | cm | ||
| φ | rad | –1.355×10–20 | rad | |||
| Qz | kG | –3.760×103 | N | |||
| My | 6.30×104 | 6.30×104 | kG·m | –6.297×105 | N·cm | |
| θ | rad | 1.084×10–19 | rad | |||
| Tt | kG·m | 9.095×10–13 | N·cm | |||
| Bω | –4.46×103 | 4.47×103 | kG·m2 | –4.493×104 | N·cm2 | |
| Tω | kG·m | –3.492×102 | N·cm | |||
| Tsum | kG·m | –3.492×102 | N·cm |