Järgmine: D.3 Jäiga keha pööre Üles: D. Vektorite teisendused Eelmine: D.1 Kohalik ja üldteljestik
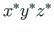 kohalikud koordinaadid. Vaatleme veel parema käe kolmikuid
kohalikud koordinaadid. Vaatleme veel parema käe kolmikuid
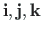 ja
ja
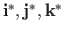 .
Need on ühikvektorite kolmikud, mis määravad
koordinaattelgede suuna.
Joonisel D.1 on ühikvektorid
.
Need on ühikvektorite kolmikud, mis määravad
koordinaattelgede suuna.
Joonisel D.1 on ühikvektorid
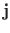 ja
ja
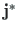 suunatud vaataja poole. Vektori
suunatud vaataja poole. Vektori
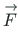 projektsioonid
telgedele x, z on
projektsioonid
telgedele x, z on 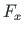 ,
, 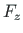 , telgedele
, telgedele
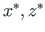 aga
aga
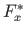 ,
,
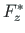 . Seega
. Seega
Korrutame avaldise (D.1) vektoritega
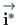 ja
ja
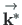 . Võtame arvesse, et risti olevate vektorite
skalaarkorrutis (sisekorrutis) on null.
Saame
. Võtame arvesse, et risti olevate vektorite
skalaarkorrutis (sisekorrutis) on null.
Saame
Pöördseoste leidmiseks korrutame avaldist (D.1) vektoritega
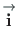 ja
ja
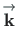 :
:
Ühikvektorite skalaarkorrutis võrdub nende positiivsete suundade vahelise nurga koosinusega:
Telje 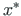 suunakoosinused tähistame järgmiselt:
suunakoosinused tähistame järgmiselt:
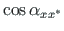 =
=
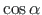 ja
ja
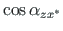 =
= 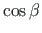 (
(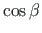 =
=
 =
=
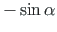 ).
Jooniselt D.1 näeme, et
).
Jooniselt D.1 näeme, et
Suunakoosinused arvutame varda lõpu ja alguse koordinaatide
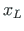 ,
, 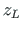 ,
, 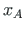 ,
, 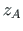 (jn D.2) järgi:
(jn D.2) järgi:
Nüüd avaldame koordinaatide teisenduse:
Koordinaatide pöördteisendus:
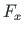 ja
ja 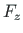 võrrandis
(D.9) nende avaldistega võrrandis
(D.10), saame maatrikskorrutise
võrrandis
(D.9) nende avaldistega võrrandis
(D.10), saame maatrikskorrutise
Arvestades, et 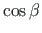 =
=
 =
=
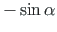 , võime seosed (D.9) kirjutada kujul
, võime seosed (D.9) kirjutada kujul
Koordinaatide teisendus pöördel nurga 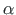 võrra:
võrra:
- ümber 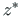 -telje
-telje
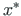 -telje
-telje
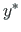 -telje
-telje
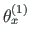 ja paindenurga
vektor
ja paindenurga
vektor
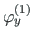 . Kohalike koordinaatide
. Kohalike koordinaatide 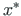 ,
, 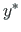 pöördel ümber
pöördel ümber 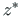 -telje nurga
-telje nurga 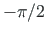 võrra
võrra
Murdepunktis peavad olema tasakaalus koguväändemomendi vektor
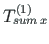 ja paindemomendi vektor
ja paindemomendi vektor
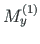 ning vektorid
ning vektorid
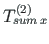 ja
ja
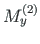 :
:
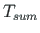 koosneb vabaväändemomendist
koosneb vabaväändemomendist 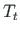 ja
kooldeväändemomendist
ja
kooldeväändemomendist
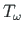 (
(
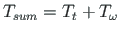 ),
saame sõlme tasakaaluvõrranditeks
),
saame sõlme tasakaaluvõrranditeks
andres