Järgmine: D.4 Kvaasi- ja semitangentsiaalsed Üles: D. Vektorite teisendused Eelmine: D.2 Koordinaatide teisendus
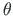 ,
, 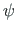 ja
ja 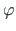 [LR71]. Vaatleme üldist (globaalset)
Cartesiuse ristkoordinaadistikku
[LR71]. Vaatleme üldist (globaalset)
Cartesiuse ristkoordinaadistikku 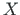 ,
, 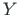 ,
, 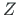 ja kohalikku (lokaalset) ristkoordinaadistikku
ja kohalikku (lokaalset) ristkoordinaadistikku 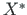 ,
, 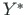 ,
, 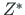 , mis on seotud jäiga kehaga. Tasandite
, mis on seotud jäiga kehaga. Tasandite 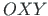 ja
ja
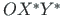 lõikejoont
lõikejoont 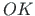 nimetatakse sõlmjooneks. Positiivse suuna sõlmjoonel määrame nii, et pöördel
nimetatakse sõlmjooneks. Positiivse suuna sõlmjoonel määrame nii, et pöördel 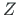 -teljelt
-teljelt
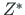 -teljele väiksemat nurka
-teljele väiksemat nurka 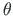 mööda tekiks parema käe teljestik.
mööda tekiks parema käe teljestik.
Euleri nurkade jaoks on kasutusele võetud erinimetused, mis on pärit astronoomiast. Nii nimetatakse
nurka 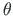 nutatsiooninurgaks, nurka
nutatsiooninurgaks, nurka 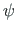 pretsessiooninurgaks
ja nurka
pretsessiooninurgaks
ja nurka 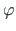 omapöördenurgaks. Analoogilised nimetused on ka telgedel, mille
ümber nimetatud pöörded toimuvad:
omapöördenurgaks. Analoogilised nimetused on ka telgedel, mille
ümber nimetatud pöörded toimuvad: 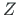 -telge nimetatakse pretsessiooniteljeks, sõlmjoont
-telge nimetatakse pretsessiooniteljeks, sõlmjoont 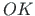 nutatsiooniteljeks ja
nutatsiooniteljeks ja 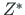 -telge omapöörlemisteljeks.
-telge omapöörlemisteljeks.
Lineaarses paindeteoorias vaadeldakse pöördenurki fikseeritud telgede suhtes. Näitame, et suurte (lõplike) pöördenurkade puhul ei kehti pöörete kommutatiivsus.
Võrdleme joonisel D.4 näidatud pöördeid x- ja y-telje
ümber. Joonisel D.4 a teeme pöörded
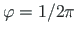 ja
ja
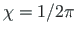 ümber y- ja x-telje, joonisel D.4 b pöörded
ümber y- ja x-telje, joonisel D.4 b pöörded
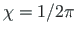 ja
ja
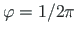 ümber x- ja y-telje. Pöörete algasendid on samad,
lõppasendid aga erinevad, seega pöörded ümber fikseeritud telgede ei ole vahetatavad,
kommutatiivsed [Arg82].
ümber x- ja y-telje. Pöörete algasendid on samad,
lõppasendid aga erinevad, seega pöörded ümber fikseeritud telgede ei ole vahetatavad,
kommutatiivsed [Arg82].
Edasi vaatleme jäika keha, millele mõjub moment y-telje suhtes
(jn D.5 a). Pöördel 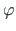 ümber y-telje teeb moment
ümber y-telje teeb moment 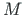 positiivset tööd
positiivset tööd
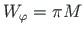 . Jäiga keha sama lõppasendi (jn D.5 b) saame pööretega
. Jäiga keha sama lõppasendi (jn D.5 b) saame pööretega 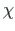 ja
ja 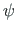 ümber x- ja z-telje. Viimati vaadeldud pööretel moment
ümber x- ja z-telje. Viimati vaadeldud pööretel moment 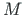 tööd ei tee, s.t
tööd ei tee, s.t
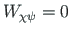 . Nii sõltub töö fikseeritud telgede puhul tee (pöördenurkade)
kujust ja on mittekonservatiivne [Zie77].
. Nii sõltub töö fikseeritud telgede puhul tee (pöördenurkade)
kujust ja on mittekonservatiivne [Zie77].
andres