Järgmine: D.5 Kvaasi- ja semitangentsiaalsed Üles: D. Vektorite teisendused Eelmine: D.3 Jäiga keha pööre
Kvaasitangentsiaalne moment
Vaatleme kvaasitangentsiaalse momendi rakendust (jn D.6 a). Võtame kasutusele jäiga jõuõla,
mis on risti varda teljega. Jõuõla suuna määrb ühikvektora 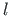 . Rakendame varda ristlõikesse jõupaari
. Rakendame varda ristlõikesse jõupaari
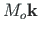 .
.
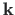 ja
ja
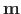 on risti.
on risti.
Rakendame varda otsa väikese pöörde
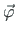 . Uueks jõuõlaks saab
. Uueks jõuõlaks saab
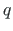 osutab siin kvaasitangentsiaalsele momendile.
osutab siin kvaasitangentsiaalsele momendile.
Semitangentsiaalne moment
Vaatleme semitangentsiaalse momendi
rakendust (jn D.6 b), kus
momendil on kaks teineteisega risti olevat jõuõlga.
Rakendatav moment
Rakendame varda otsa pöörde
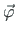 , jättes momendid
, jättes momendid
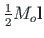 ja
ja
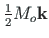 konstantseks. Jõuõlg (vektor)
konstantseks. Jõuõlg (vektor)
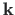 muutub nii nagu
muutub nii nagu
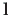 (D.25):
(D.25):
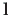 ,
,
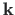 ja
ja
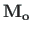 avaldised (D.25), (D.29), (D.28) võrrandisse
(D.30), saame
avaldised (D.25), (D.29), (D.28) võrrandisse
(D.30), saame
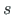 osutab siin semitangentsiaalsele momendile.
osutab siin semitangentsiaalsele momendile.
Jälgiva momendi 7.3 (ingl follower moment) juurdekasv
Joonisel:
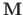 – moment ümber fikseeritud telje Lagrange'i koordinaatides;
– moment ümber fikseeritud telje Lagrange'i koordinaatides;
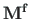 – moment kaasaliikuvates Lagrange'i koordinaatides;
– moment kaasaliikuvates Lagrange'i koordinaatides;
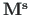 – momentide
– momentide
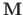 ,
,
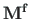 aritmeetiline keskmine:
aritmeetiline keskmine:
andres