Järgmine: D.6 Pseudovektor Üles: D. Vektorite teisendused Eelmine: D.4 Kvaasi- ja semitangentsiaalsed
Semitangentsiaalse pöörde kommutatiivsus
Semitangentsiaalsete pöörete järjestuse kirjeldamiseks kasutame tähistust
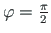
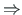
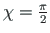 ;
;
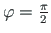
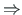
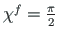 ;
;
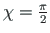
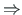
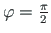 .
.
Näitame, et semitangentsiaalsete pöörete järjestusest
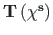
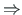
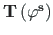 või
või
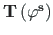
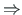
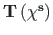 ei sõltu lõpptulemus:
ei sõltu lõpptulemus:
Semitangentsiaalsete pöörete reeglid
Semitangentsiaalsete pöörete puhul tuleb vahet teha järgmistel juhtudel (jn D.10):
Alustame lihtsaima juhuga, kus koordinaadid pöörduvad, kuid ristlõige ei pöördu.
Koordinaatide teisendus tehakse vektoritega
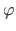 =
=
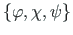 ja
ja
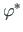 =
=
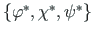 .
.
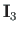 on
on 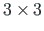 ühikmaatriks ja
ühikmaatriks ja
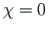 ,
,
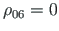 (jn D.10 a) teeme teisenduse
(jn D.10 a) teeme teisenduse
Koordinaatide ja ristlõike samaaegsel pöördumisel
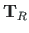 on antud avaldisega (D.39).
Tasandilisel juhul
on antud avaldisega (D.39).
Tasandilisel juhul
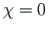 ,
,
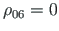 (jn D.10 b)
(jn D.10 b)
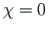 ,
,
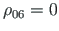 (jn D.10 c) teeme teisenduse
(jn D.10 c) teeme teisenduse
andres