Järgmine: 3.1 Rajatingimused Üles: Tabelid Eelmine: 2.3.1.8 Laus- ja koondkoormus
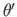 . Väändenurk
. Väändenurk 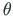 ja kooldumine
ja kooldumine
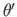 on omavahel seotud.
on omavahel seotud.
Vaatleme kooldumist õhukeseseinaliste talade ühendamisel sõlmes. Piirdume süsteemiga, kus talade ristlõigete pinnakeskmed asuvad
ühisel tasandil. Samuti asuvad ühisel tasandil talade elastsed teljed .
Punkti, kus elastsed teljed lõikuvad, nimetame sõlme keskmeks (ingl joint center, vn 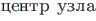 ). Selleks et sõlmes ühendatavate talade kooldumus
). Selleks et sõlmes ühendatavate talade kooldumus
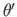 oleks võrdne,
peaksid talade ristlõigete sektorkoordinaatide
oleks võrdne,
peaksid talade ristlõigete sektorkoordinaatide 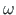 tuletised, s.t sektorkoordinaatide epüüride puutujad
(
tuletised, s.t sektorkoordinaatide epüüride puutujad
(
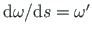 ), olema kontaktpunktis võrdsed [Bõt62].
), olema kontaktpunktis võrdsed [Bõt62].
Vaatleme õhukeseseinalise tala (jn 3.1 a) ristlõike punkti
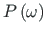 pikisiiret
pikisiiret 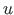 . Pikisiirde
. Pikisiirde 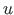 saame määrata avaldisega
saame määrata avaldisega
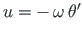 (1.12), kus
(1.12), kus 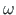 on punkti
on punkti
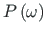 sektorkoordinaat (
sektorkoordinaat (
 ). Tähistame ülemise vöö pöördenurga ümber z-telje sümboliga
). Tähistame ülemise vöö pöördenurga ümber z-telje sümboliga 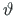 .
Ristlõike punkti
.
Ristlõike punkti
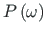 pikisiirde saame avaldada korrutisena
pikisiirde saame avaldada korrutisena
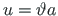 , kus
, kus 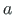 on punkti kaugus z-teljest.
Kui võtta suhteline väändenurk võrdseks ühega (
on punkti kaugus z-teljest.
Kui võtta suhteline väändenurk võrdseks ühega (
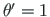 ), siis avaldisest (1.12) saame
), siis avaldisest (1.12) saame
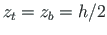 , siis
, siis
Õhukeseseinaliste varraste liitekoht võib deformeeruda [MW03]. Kui varraste ühendamisel sõlmes ristlõige moondub (jn 3.1 b), siis tuleb valida sobivad kinemaatilised pidevustingimused [DK90].
Suurte pöördenurkade (väändenurkade) kirjeldamiseks kasutatakse pöörde pseudovektorit (D.46) [Teh05].
Õhukeseseinalisi varrassüsteeme arvutatakse ka jõumeetodiga ja deformatsioonimeetodiga [BC09], [Bõt62]. Jõumeetodi puhul on lisatundmatuteks jõud, mis leitakse kinemaatilistest pidevustingimustest. Deformatsioonimeetodi korral on tundmatuteks siirded ja pöörded, mis leitakse sõlmede tasakaalutingimustest. EST-meetodiga arvutamisel leitakse siirded, pöörded, jõud ja momendid varraste otstes samaaegselt. Selle meetodiga rajaülesannet lahendades kasutatakse kinemaatilisi pidevustingimusi ja tasakaalutingimusi.
Jätkuvtala kinemaatilisi pidevustingimusi kirjeldame näites 3.1.
Joonisel 3.2 kujutatud jätkuvtala toesidemed takistavad väänet
3.1 (väändenurk
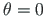 ).
).
Joonisel 3.3 on kujutatud elastsete tugedega 3.2 3.3 jätkuvtala. Väändenurga ja paindenurga pidevustingimust on vaadeldud näites 3.2 ,,L-tala arvutus ülekandevõrranditega".