Järgmine: D.6.2 Üksik pseudovektor Üles: D.6 Pseudovektor Eelmine: D.6 Pseudovektor
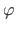 ,
, 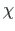 ,
, 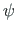 on pöörde
on pöörde
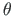 komponendid
ristkoordinaadistikus
komponendid
ristkoordinaadistikus 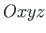 .
.
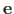 on pöörde teljesuunaline ühikvektor (jn D.11).
on pöörde teljesuunaline ühikvektor (jn D.11).
Pöörete abimaatriks on
Leiame pöörete teisendusmaatriksi
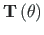 nii, et kohavektor
nii, et kohavektor
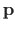 pöörduks uude asukohta
pöörduks uude asukohta
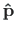 (jn D.11):
(jn D.11):
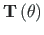 on mittelineaarne
funktsioon pöördest
on mittelineaarne
funktsioon pöördest 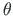 .
.
Normeerime pöörete pseudovektori nii:
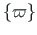 on pöörde pseudovektor pikkusega
on pöörde pseudovektor pikkusega
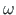 ja komponentidega
ja komponentidega
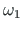 ,
,
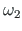 ja
ja
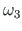 .
Kasutame Rankini ja Brogani [RB86] normaliseerimist
.
Kasutame Rankini ja Brogani [RB86] normaliseerimist
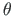 ja
ja 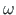 :
:
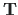 [RB86] on seoses pöördega
[RB86] on seoses pöördega
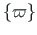 või pöördega
või pöördega
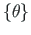 .
.
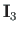 on
on
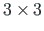 ühikmaatriks ja
ühikmaatriks ja 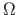 pöörete abimaatriks:
pöörete abimaatriks:
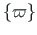 avaldisest
avaldisest
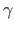 on maatriksi
on maatriksi
![$ \left[\mathbf{T}\right]$](imgLsD1257.png) jälg:
jälg: