Järgmine: D.6.3 Suured pöörded ja Üles: D.6 Pseudovektor Eelmine: D.6.1 Suurte pöörete maatriksesitus
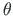 .
.
Määrame pseudovektori 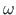 :
:
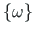 vastava abimaatriksi:
vastava abimaatriksi:
Vaatleme joonist D.12, kus punkt 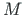 on lõigu
on lõigu
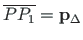 keskpunkt.
Lõik
keskpunkt.
Lõik
Et lõik
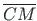 on risti lõiguga
on risti lõiguga
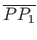 , siis
, siis
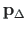 on risti pseudovektoriga
on risti pseudovektoriga 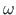 ja
ja
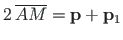 , siis langeb ta kokku vektorkorrutisega
, siis langeb ta kokku vektorkorrutisega
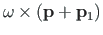 . Arvestades, et pseudovektori
. Arvestades, et pseudovektori
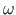 ja lõigu
ja lõigu
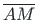 vaheline nurk on
vaheline nurk on 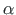 , saame
vektorkorrutise
, saame
vektorkorrutise
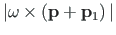 suuruseks
suuruseks
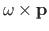 ja
ja
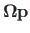 samaväärsuses.
samaväärsuses.
andres