Järgmine: E. Arvutiprogrammid Üles: D.6 Pseudovektor Eelmine: D.6.2 Üksik pseudovektor
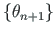 eelmisest pseudovektorist
eelmisest pseudovektorist
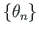 juurdekasvu (inkremendi)
juurdekasvu (inkremendi)
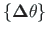 abil.
Argyris [Arg82] kasutas pöörete pseudovektori moodustamiseks
kvaternioone7.4.
abil.
Argyris [Arg82] kasutas pöörete pseudovektori moodustamiseks
kvaternioone7.4.
Kvaternioonide [BŠ73] mõiste võttis kasutusele
W. R. Hamilton7.5 1843. aastal. Kvaternioonid 7.6
on defineeritud skaalari ja vektori summana [ANS92]:
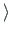 tähistavad kvaterniooni. Kvaterniooni
tähistavad kvaterniooni. Kvaterniooni 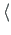 q
q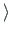 skalaarne ja vektoriaalne osa on
skalaarne ja vektoriaalne osa on 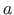 ning
ning
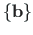 .
Kvaterniooni
.
Kvaterniooni 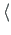 q
q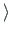 norm
norm
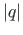 arvutatakse järgmiselt:
arvutatakse järgmiselt:
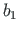 ,
, 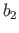 ja
ja 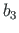 on vektori
on vektori
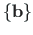 komponendid. Kui
komponendid. Kui
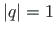 , siis
, siis 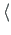 q
q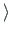 on ühikkvaternioon.
on ühikkvaternioon.
 ja
ja
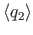 kaks kvaterniooni:
kaks kvaterniooni:
 avaldub viisil
avaldub viisil
 skalaarne
skalaarne
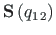 ja vektoriaalne
ja vektoriaalne
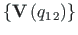 osa:
osa:
 q
q ühikkvaternioon. Avaldiste
(D.52), (D.50) abil saame pseudovektori
(D.72) kujul
ühikkvaternioon. Avaldiste
(D.52), (D.50) abil saame pseudovektori
(D.72) kujul
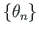 ja
ja
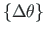 :
:
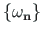 on normaliseeritud
on normaliseeritud
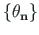 ja
ja
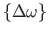 on
normaliseeritud
on
normaliseeritud
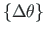 .
.
Pseudovektori
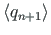 moodustamiseks kasutatakse kvaternioonide
korrutamist (D.69):
moodustamiseks kasutatakse kvaternioonide
korrutamist (D.69):
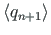 on ühikvektor, sest
on ühikvektor, sest
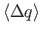 ja
ja
 on ühikkvaternioonid. Pseudovektori
on ühikkvaternioonid. Pseudovektori
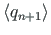 saab esitada kahel viisil:
saab esitada kahel viisil:
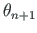 ja
ja
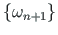 leiame
võrranditest (D.79) ja (D.80).
leiame
võrranditest (D.79) ja (D.80).
Tuleb arvestada, et nurk 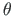 on piiratud pöördega
on piiratud pöördega 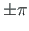 . See piirang
tuleneb siinusest, mille määramispiirkond on
. See piirang
tuleneb siinusest, mille määramispiirkond on 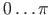 . Kui
. Kui
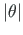 on suurem kui
on suurem kui 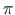 , siis
, siis
andres