Переменные

В ходе программирования обычно необходимо запоминать некоторое количество данных (промежуточные результаты, произошедшие события, входные данные, выходные данные и т.д.). Эти значения приходится держать в памяти. Для этого объявляется место в памяти, которое используется для хранения данных и это объявленное место называется переменной. Поскольку данные, которые хранятся, могут быть самыми разными, то при объявлении переменной, объявляется и тип данных, которые будут храниться в этой переменной (тип переменной).

Простые типы

У переменной простого типа под ключевым словом скрывается одно значение (зачастую читаемое как число)  и к нему есть прямой доступ. Наиболее известные простые типы это: целое число со знаком, целое число без знака, дробное число (с запятой), символ, логическое значение. В различных языках они могут немного отличаться.

Структурированные типы

В случае структурированных типов под одним ключевым словом группируются несколько совместных значений, таких например как координаты точки или имя и фамилия человека. В таком виде набор данных разом легче передавать. В то же время  использовать или изменять данные внутри структуры приходиться по одному.

Массивы

Массив это набор данных одинакового типа, у которых одно имя и которые отделяются друг от друга при помощи индекса. Массивы значительно облегчают обработку однотипных данных. Простота обработки является результатом того, что в ходе выполнения программы можно просто менять индекс и таким образом проще обращаться к необходимой переменной. Получение значения переменной из массива при помощи порядкового номера является для компьютера довольно быстрой задачей.

Массивы могут быть одномерными (ряд, строка), двумерными(таблица, матрица), трёхмерными(куб) и т.д.

Пример (С#, Java)

int[] mass = new int[10]; //создаётся массив для хранения десяти целых чисел

mass[0]=1; //по индексу 0 записывается значение 1

Дополнительное чтение: http://enos.itcollege.ee/~jpoial/java/i200loeng4.html

Записи

Для хранения данных разных типов, которые вместе образуют некий связанный набор, используются записи. Например, запись человека формируется из следующих данных: имя(текст), фамилия(текст), пол(логическое значение, 0 - женщина, 1 - мужчина), вес(дробное число). Эти данные образуют одно целое при описании одного человека, однако, сами по себе очень разных типов.

Пример (C#)

        struct inimene {

     public string eesnimi;

     public string perenimi;

     public bool sex;

     public float weight;

        }

С помощью этой записи мы можем создать переменную kasutaja(пользователь) и  присвоить пользователю значения имени, фамилии, пола и веса:

        inimene kasutaja;

        kasutaja.eesnimi = "Jaan";

        kasutaja.perenimi = "Mets";

        kasutaja.sex = 1;

        kasutaja.weight = 80.0;

Списки и деревья

В настоящее время часто для хранения данных используются списки (англ. List). Если каждый элемент списка указывает на следующий за ним элемент, то это связанный список, конец такого списка обозначается пустым элементом (null). Связанный список, где каждый элемент указывает только на следующий за ним, называется однонаправленным списком. Связанный список, где каждый элемент указывает на следующий и предыдущий элементы, называется двунаправленным. Связанный список, где отсутствуют первый и последний элементы, и каждый элемент указывает на следующий, называется кольцевым списком. Длина связанного списка определяется количеством его элементов. Первый элемент списка это голова  (англ. Head) и остальные элементы - хвост (англ. Tail).

Стек (англ. Stack) это связанный список, в котором элемент добавленный последним - читается первым(англ. LIFO -  Last In First Out (последним вошёл первым вышел)).

Очередь (англ. Queue) это связанный список, в котором элемент, добавленный первым - читается первым (англ. FIFO - First In First Out(первым вошёл, первым вышел)).

Дополнительное чтение: http://www.cs.tlu.ee/~inga/alg_andm/linked_list_C_2011.pdf

Дерево - это стрктура данных, в которой данные размещаются в виде дерева, состоит из вершин (англ. Node) и дуг (англ. Edges), которые соединяют вершины (указатели). Вершины, которые соединены дугами с вершиной расположенной выше называются детьми (англ. Childs), а расположенная выше вершина в этом случае является родителем (англ. Parent). Самая верхняя вершина - это корень (англ. Root). Вершину, у которой нет детей, называют листом (англ. Leaf).

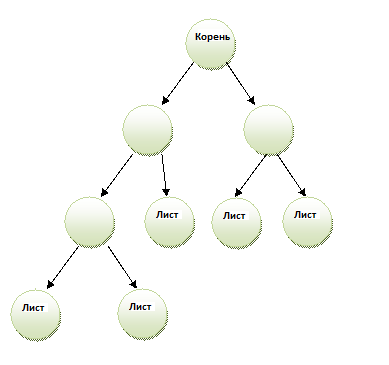
Двигаясь от вершины к родителю, а оттуда к следующему родителю и т.д. достигаем корня. Предками называются все вершины находящиеся на пути от рассматриваемой вершины до корня. Высота дерева (англ. tree height) определяется самым длинным путём от листа к корню.

В случае упорядоченного дерева, корень и соединённые непосредственно с ним вершины определены, как вершины первого уровня (англ. First level nodes)(дети корня), а вершины соединённые напрямую с вершинами первого уровня - это вершины второго уровня (дети вершин первого уровня) и т.д.; также важным считается порядок детей слева на право.

Дополнительное чтение: http://www.cs.tlu.ee/~inga/alg_andm/tree_gen_2011.pdf

 

Двоичное дерево - это такое дерево, в котором у каждого родителя может быть один ребёнок, два ребёнка или совсем не быть детей и порядок детей важен.

Двоичное дерево поиска (англ. Binary search tree) - это двоичное дерево, которое упорядочено. Слева от вершины всегда находиться число меньшего размера и справа всегда большего.

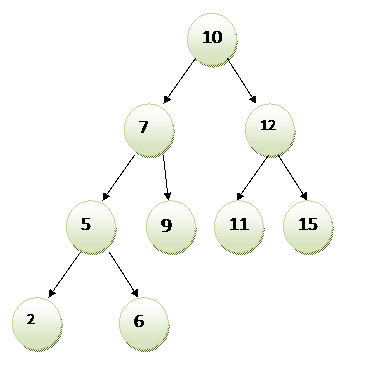
При поиске по такому дереву искомое значение сравнивается с корнем и если искомое равно корню, то оно существует и найдено. Если искомое значение не равно корню, то операция сравнения продолжается дальше, соответственно сравнивая искомое с набором вершин, находящихся справа или слева до тех пор, пока не доходят до листьев. Если искомое значение равно значению одной из вершин, то искомый элемент найден и существует, однако если такой вершины не найдётся, то искомого элемента в данном дереве не существует. Такой способ поиска в разы быстрее, чем полный обход массива или связанного списка.

Б-дерево (англ. B tree) это дерево поиска, в котором количество детей у каждой вершины находится в промежутке от (t-1) до (2t-1), где t - это любая константа.

Б*-дерево - это Б-дерево, в котором вершины заполняются на 2/3, вначале заполняя две дочерние вершины путём перераспределения ключей и разбивая их после этого на 3 вершины.

За счёт этого Б-дерево позволяет сохранять глубину дерева меньше чем у бинарного дерева. Ограничивая заполнение, также есть возможность на промежуточных уровнях удерживать объем используемой памяти в чётко определённых пределах и в то же время можно сразу добавлять данные в подходящее место.

Дополнительное чтение: http://enos.itcollege.ee/~jpoial/algoritmid/puustruktuurid.html